QuestionPapersHub.com
GATE-2019
Q: An array of 25 distinct elements is to be sorted using quicksort. Assume that the pivot element is chosen uniformly at random. The probability that the pivot element gets placed in the worst possible location in the first round of partitioning (rounded off to 2 decimal places) is ________.
GATE-2019
Q: Consider a sequence of 14 elements: A = [−5, −10, 6, 3, −1, −2, 13, 4, −9, −1, 4, 12, −3, 0]. The subsequence sum S(i,j)=∑jk=iA[k] . Determine the maximum of S(i,j), where 0≤i≤j<14. (Divide and conquer approach may be used.) ________.
GATE-2019
Q: There are n unsorted arrays: A1, A2, …, An. Assume that n is odd. Each of A1, A2, …, An contains n distinct elements. There are no common elements between any two arrays. The worst-case time complexity of computing the median of the medians of A1, A2, …, An is
- A: O(n)
- B: O(nlogn)
- C: O(n2)
- D: Ω(n2logn)
GATE-2019
Q: Let G be any connected, weighted, undirected graph.
Q: Let G be any connected, weighted, undirected graph.
I. G has a unique minimum spanning tree, if no two edges of G have the same weight.
II. G has a unique minimum spanning tree, if, for every cut of G, there is a unique minimum-weight edge crossing the cut.
Which of the above two statements is/are TRUE?
- A: I only
- B: II only
- C: Both I and II
- D: Neither I nor II
GATE-2018
Q: Let G be a simple undirected graph. Let TD be a depth first search tree of G. Let TB be a breadth first search tree of G. Consider the following statements.
Q: Let G be a simple undirected graph. Let TD be a depth first search tree of G. Let TB be a breadth first search tree of G. Consider the following statements.
(I) No edge of G is a cross edge with respect to TD. (A cross edge in G is between two nodes neither of which is an ancestor of the other in TD.)
(II) For every edge (u,v) of G, if u is at depth i and v is at depth j in TB, then |i-j| = 1.
Which of the statements above must necessarily be true?
- A: I only
- B: II only
- C: Both I and II
- D: Neither I nor II
GATE-2018
Q: Let G be a graph with 100! vertices, with each vertex labelled by a distinct permutation of the numbers 1,2, … , 100. There is an edge between vertices u and v if and only if the label of u can be obtained by swapping two adjacent numbers in the label of v. Let y denote the degree of a vertex in G, and z denote the number of connected components in G. Then, y + 10z = _____.
GATE-2018
Q: Assume that multiplying a matrix G1 of dimension p×q with another matrix G2 of dimension q×r requires pqr scalar multiplications.
Computing the product of n matrices G1G2G3...Gn can be done by parenthesizing in different ways. Define GiGi+1 as an explicitly computed pair for a given paranthesization if they are
directly multiplied. For example, in the matrix multiplication chain G1G2G3G4G5G6 using parenthesization (G1(G2G3))(G4(G5G6)),G2G3 and G5G6 are the only explicitly computed pairs.
Q: Assume that multiplying a matrix G1 of dimension p×q with another matrix G2 of dimension q×r requires pqr scalar multiplications.
Computing the product of n matrices G1G2G3...Gn can be done by parenthesizing in different ways. Define GiGi+1 as an explicitly computed pair for a given paranthesization if they are
directly multiplied. For example, in the matrix multiplication chain G1G2G3G4G5G6 using parenthesization (G1(G2G3))(G4(G5G6)),G2G3 and G5G6 are the only explicitly computed pairs.
Consider a matrix multiplication chain F1F2F3F4F5, where matrices F1,F2,F3,F4 and F5 are of dimensions 2×25,25×3,3×16,16×1, and 1×1000, respectively. In the parenthesization of F1F2F3F4F5 that minimizes the total number of scalar multiplications, the explicitly computed pairs is/are
- A: F1F2 and F3F4 only
- B: F2F3 only
- C: F3F4 only
- D: F1F2 and F4F5 only
GATE-2017
Q: Let G= (V,E) be any connected undirected edge-weighted graph. The weight of the edges in E are positive and distinct. Consider the following statements:
Q: Let G= (V,E) be any connected undirected edge-weighted graph. The weight of the edges in E are positive and distinct. Consider the following statements:
(I) Munimum Spanning Tree of G is always unique.
(II) shortest path between any two vertices of G is always unique.
Which of the above statements is/are necessarily true?
- A: (I) only
- B: (II) only
- C: both (I) and (II)
- D: neither (I) nor (II)
GATE-2017
Q: Let A be an array of 31 numbers consisting of a sequence of 0's followed by a sequence of 1's. The Problem is to find the smallest index i such that A[i] is 1 by probing the minimum number of locations in A. The worst case number of probes performed by an optimal algorithm is _________
GATE-2017
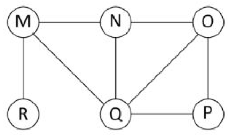
Q: The Breadth First search (BFS) algorithm has been implemented using the queue data structure. Which one of the following is a possible order of visiting the nodes in the graph below?

- A: MNOPQR
- B: NQMPOR
- C: QMNROP
- D: POQNMR