Yes, it is true that algebra is not that easy subject for every student due to their changing mindsets. But let us tell you that it is not rocket science either. All you need to do is to play with a combination of variables, expressions, and polynomials, just by applying various algebraic techniques to them. Various tools and applications have been developed to reduce complexity in resolving algebraic problems. An online synthetic division calculator by calculator-online.net is one such tool.
This online free calculator is no doubt a gift for those pupils seeking an angel coming down and providing them with fast solutions to their dairy-based mathematical problems. With the help of this synthetic substitution calculator, it has now become very easy to substitute a particular variable value in an algebraic polynomial to get its fast outcomes.
So what about knowing more about synthetic division? Anxious enough? Even we are as well! Let us dive into it!
What Is Synthetic Division?
“A particular method in which a polynomial is factorized by a linear factor.”
A synthetic division is regarded as the shortcut method of the polynomial long division method. Where the long algebraic polynomials are divided by one another in a polynomial long division method, they are divided by the short linear factor in the synthetic division process. For instance, a free synthetic division calculator with steps allows determining the factors of a polynomial that satisfy it properly.
Zeros of a Polynomial:
Zeroes are termed roots of the equation. Just suppose the following generic function below:
Y = f(x)
For this function above, the values that fully satisfy the ranges defined by the domain of the function are called the roots or zeros of the function.
Real Zeroes:
The x-intercepts of the graphs are represented by real zeros, which are the values of x when y equals zero.
Complex Zeros:
Complex zeros are x values when y equals zero, however they are not visible on the graph. Complex zeros are made up of imaginary numbers.
Example:
This section is focused on seeing. Because here we will be resolving an example to find the zero/es of the polynomial by using the synthetic division technique. Let’s go!
Problem:
Determine whether the root x = 1 is a zero of the polynomial x^3 + 1 or not?
Solution:
Before getting started, let us make it clear that if the root x = 1 will create a zero remainder while dividing a polynomial x^3 + 1, then it will be called a zero of the given polynomial. You can use a synthetic substitution calculator
to instantly judge that. Anyways let us explain each and every step involved in the calculations:
Steps Involved In Calculations:
- First of all, we have to write all the missing variable coefficients in the given polynomial as follows:
Coefficient of x^3 = 1
Coefficient of x^2 = 1
Coefficient of x = 1
Constant term = -1
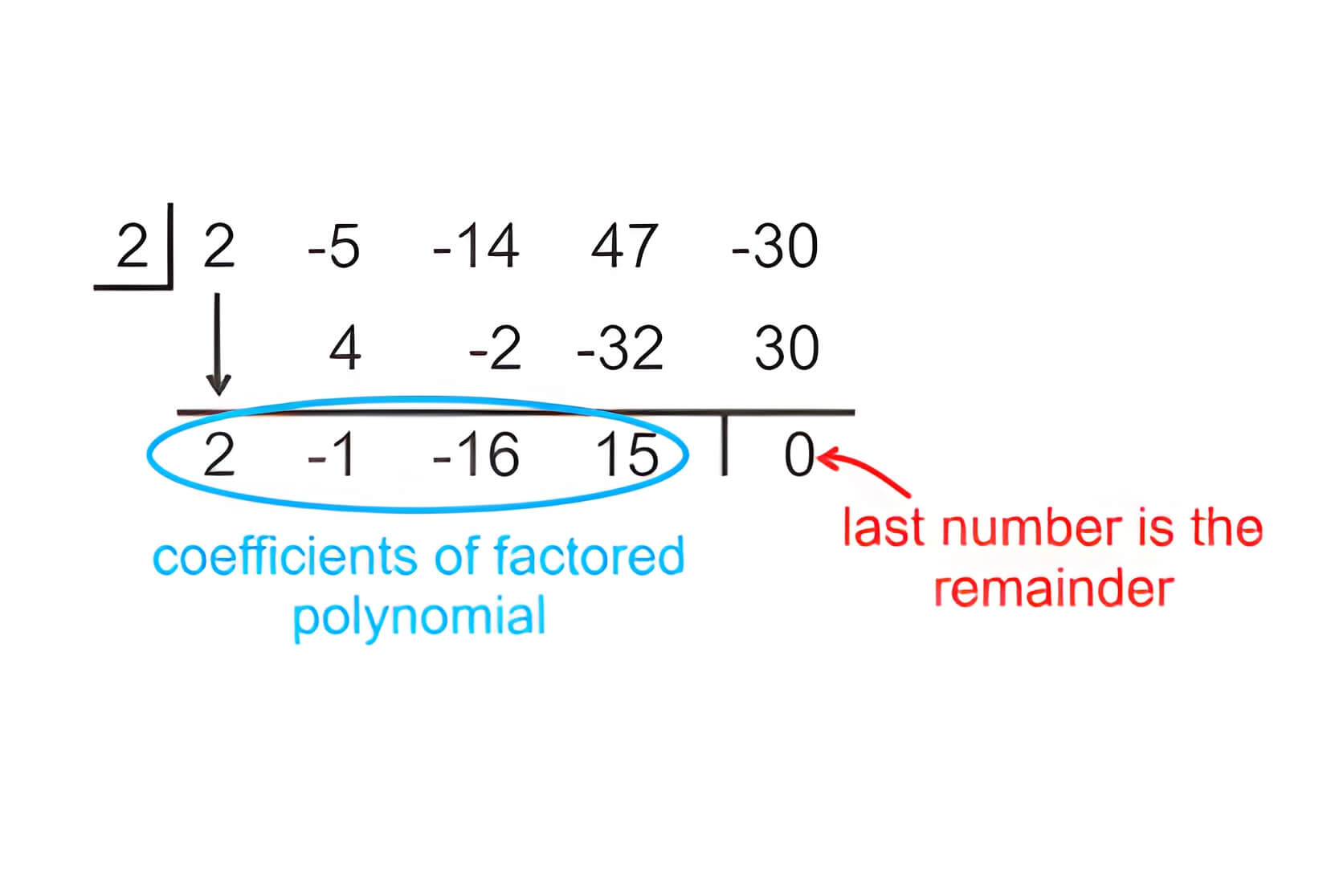
- Now, we need to write these coefficients in the form of the synthetic division as below:
- In the above picture, the number 1 on the most left is the root given, and the numbers 1, 0, 0, -1 are the coefficients of the polynomial
- What we need to do here is just to land down the first coefficient which is 1 just shown:
- After doing so, go for multiplying this landed coefficient with the factor 1. As 1 * 1 = 1, so write the resulting number just down to the next coefficient, which in our case is zero.
- The next step is to add both of these coefficients. This results in 1. Simply land down the 1 to the most down as shown.
- Here we need to again multiply the landed coefficient 1 with the factor 1 given and write the result beneath the next coefficient, which is again a 0. Adding 0 and 1 gives 1, so we have:
- As you saw we again multiplied the factor 1 by the landed coefficient 1 to get 1. This 1 when written down the last constant term -1 and added in it, it results in 0.
- The result of a zero in the answer proves that the given factor x = 1 is a zero of the given polynomial x^3 + 1.
The following example demonstrates how synthetic division is most typically used. You are given a polynomial and instructed to discover all of its zeros. You make a list of possible outcomes. The free online synthetic substitution calculator
also goes for determining the same results but in a fragment of seconds and accurately.
A Guide For Complex Roots:
Resolving polynomials involving complex zeros is the same as resolving real values of polynomials. But there is only one factor that makes them complex which is iota(𝜾). Rest all the steps for determining the complex zeros are the same as for real numbers.
Using Synthetic Division Calculator:
A special thanks to calculator-online.net that designed the special synthetic division calculator for the sake of simplifying and determining the roots of the polynomial expressions. Want to know how it actually works? Scroll down a little!
- Just write down the polynomials as dividend and divisor in the designated fields
- Now, tap the calculate button and here you go with it
- The free synthetic division calculator with steps shows a detailed calculations scenario involved and the remainders and the quotients of all the terms instantly and accurately
How fast it is!
Let’s Wind Up:
Mathematics is a subject that is not liked by every single person. This is because where one loves resolving problems, playing with formulas and terms, the other does not like this. But the time to get worried has over as the free synthetic substitution calculator
has made it possible to determine the results of any polynomial function in a glimpse of an eye. This is no doubt a great benefit for those who are willing to learn some new tricks to get a firm grip over the methodology. We hope this guidepost will help you a lot!
Good Luck!